Week 7
Trigonometry Introduction
I'm not sure of you background
in Trigonometry so I'll start fairly basic. Trig is an important area in
mathematics as trig functions model many real world phenomenon.
Back in a geometry course, you
may have been exposed to the acronym SohCahToa. It represents the basic trig
ratios of
Sine=sin=
(hence Soh)
Cosine=cos=
(hence Cah)
Tangent=tan=
(hence
Toa)
These sides are sides in a
right triangle in relation to a given angle
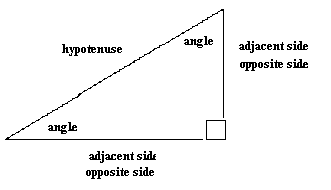
Notice how what side is
adjacent and what side is opposite changes based on which angle is being
examined.
There are also 3 other trig
ratios:
Cotangent= cot = 
= 
Cosecant = csc = 
= 
Secant= sec
= 
= 
Now to
calculate these ratios:
Suppose I have a triangle with
the following sides
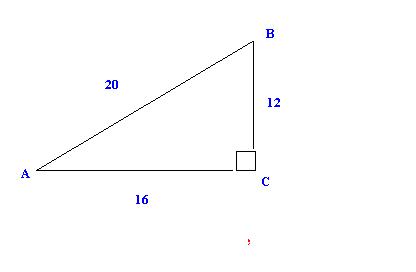
If I needed to find 
, I look at the side opposite angle A and the hypotenuse and
write them as a ratio
12/20 or 3/5 simplified. TO find the other ratios for angle A, I'll use their ratios and plug in the appropriate numbers:
|
Ratio
|
Value
|
|
Cos A
|
|
|
Tan A
|
|
|
Cot A (the reciprocal of tan
A)
|
|
|
Sec A (the reciprocal of Cos
A)
|
|
|
Csc A (the reciprocal of sin
A)
|
|
Regardless of the length of
the sides of the triangle, the trig ratios are always the same as long as the
angles are the same (similar triangles) The example I did was a 3-4-5 right
triangle. I get the same trig values for any 3-4-5 based right triangle. For
any other kind of right triangle, the results will be different.
Find the
size of the angle:
I can find out the value of
the angle (how many degrees) by finding the arcsine (pronounced "ark sine") (
) or the arccosine (
) or the arctangent (
). These buttons are on any scientific calculator, usually
above the sin, cos, and tan keys. You usually hit the second function key.
Since cos A is 0.8, type in 0.8 and hit "2nd" and
"cos" and you should get approx. 36.9 degrees. A word of caution: make sure your calculator
is in degree mode, if you want degree measures, in radian mode if you want
radian measures. This is probably one of the easiest mistakes to make.
Converting
between degrees and radians:
The text on page 394 - 395
explains this process fairly cleanly so I won't go into it here.
Degrees-Minutes-Seconds
to Decimal Degrees:
Again on page 394 in the text, there is a clear explanation of this process.
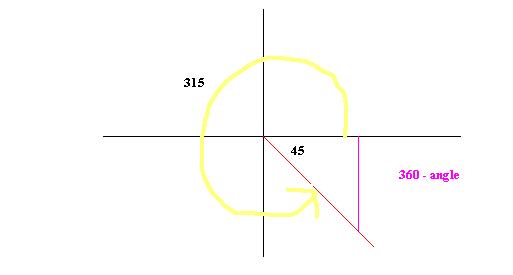
Angles of rotation:
On page 392, the text discusses positive and negative angles of rotation. Review that before you continue here. One thing the book doesn't bring out from the angles of rotation discussion is this:
Any angle of rotation can be written in terms of an acute angle. You find the acute angle as outlined below.
Second Quadrant:
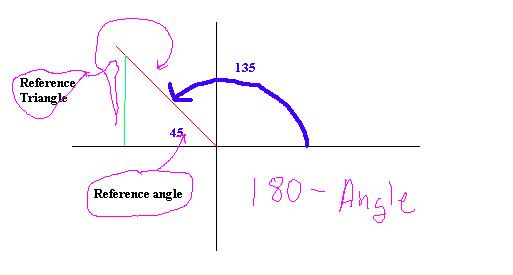
Third Quadrant:
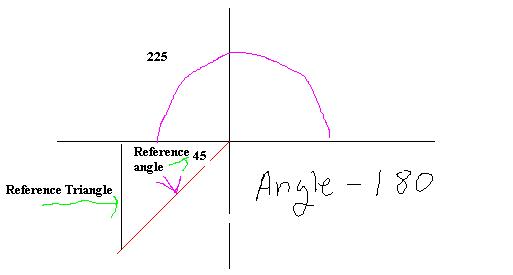
Fourth quadrant:
Finding Exact Values of trig ratios:
These are common values used throughout the rest of any mathematics courses you'll take (well, not in statistics, but anything calculus based.) We need to make a jump in how we think about the ratios. What if we place a triangle on a coordinate plane; the hypotenuse of the triangle as the radius of a unit circle (a circle with a radius of 1).
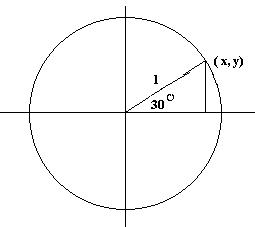
Using a little right triangle trigonometry which you did back in high school:
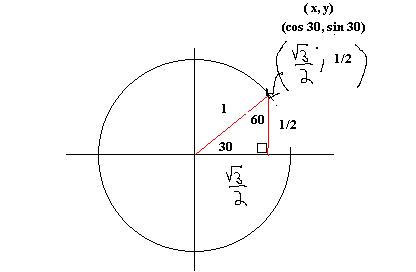
So now we have two sides of a right triangle. We can use the Pythagorean theorem to find the third side.
Since we know the opposite side is 1/2 units long and the
adjacent side is 
units long, we can
make the jump that the y coordinate is the same as the opposite side, and the x
coordinate is the same as the adjacent side (when the hypotenuse is 1). So the
point where the triangle intersects the circle is the same as the (cos A, sin
A) . This works for any triangle. For most a decimal approximation is fine. For
a 30 - 60 right triangle and an 45 - 45 right triangle we need to do a bit of
memorizing as these are common trig values that are often useful in the study
of trig functions.
For each of these, the results
are:
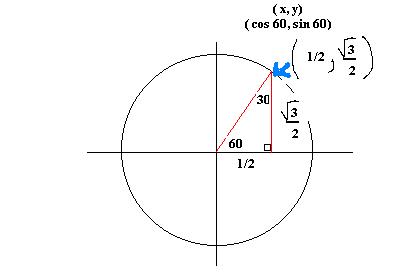
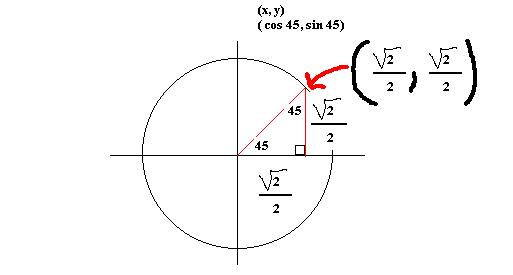
You can verify these values using right triangle trig and Pythagorean theorem.
So what about tan? Well since
tan is opposite/adjacent and the opposite is the same as sin and the adjacent
is the same as cosine, tan is 
. So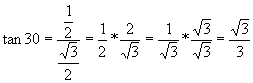 
. (I needed to rationalize the denominator, as it is
"illegal" to have a radical in the denominator of a fraction. pg. 22
in pre-req. chapter)
I can do this same thing for the other two angles and for the reciprocal functions cot, sec, and csc.
So these results can yield the table below:
|
Degree
|
radian
|
Sin
|
Cos
|
Tan
|
Cot
|
Sec
|
Csc
|
|
30
|
|
|
|
|
|
|
2
|
|
60
|
|
|
|
|
|
2
|
|
|
45
|
|
|
|
1
|
1
|
|
|
Trig
values for angles that are greater than 90 degrees (
):
Since we know these exact values for these three special angles. We can apply what we know about reference angles to angles larger than 90.
Find the exact value of sin 120:
If we make a sketch of this angle of rotation:
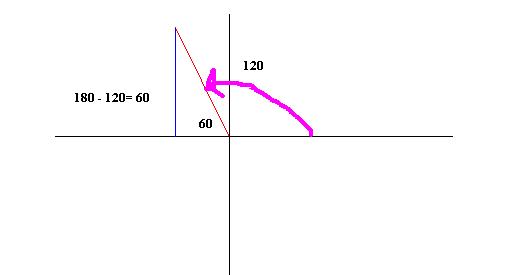
We can find the reference
angle is 60. SO the sides of the triangle and the (x, y) point on the unit
circle 
Notice that the x
value is negative (we are on the negative x axis after all. If we are thinking
of this as a length of the adjacent side, just ignore the negative). From my
work above, we know that (x, y) is the same as ( cos a , sin a). We are looking
for sin, so 
. If we were looking for cos 120 we look at the x coordinate
so cos 120 = -1/2. Because cos is always the x value, the cos is always
negative in the second quadrant. Verify this with you calculator.
What about the third quadrant?
Find tan 210:
Sketch:
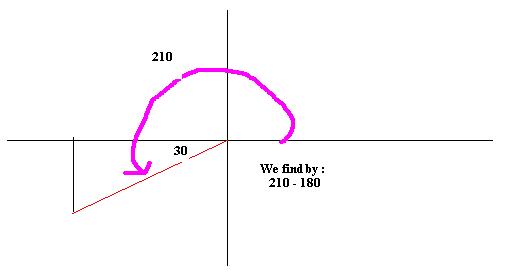
So tan 210 = tan 30. From our
table above that makes this expression equal to 
. It is positive as tan = opp/ adj. Or y/x. Since both x and
y are negative in the third quadrant, that makes this ratio positive.
For an angle in the fourth
quadrant :
Find cos 300:
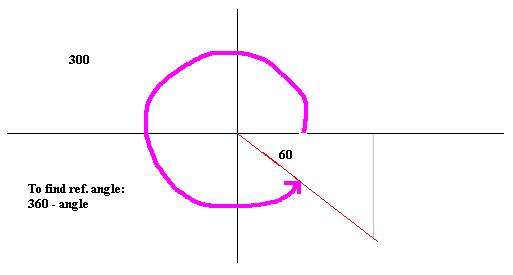
So since the reference angle
is 60, and x is positive in the 4th quadrant. Cos 300 = cos 60= 1/2.
So how do we keep straight
what is positive and what is negative:
The ACTS refers to which of the three trig ratios are
positive. For the reciprocal functions, we need to remember which are
reciprocals.
If we compile all of this
information into a table and look at all of the angles in a 360-degree angle of
rotation that have 30, 60, or 45 degree reference angle:
|
Angle
|
Sin
|
Cos
|
Tan
|
Cot
|
Sec
|
Csc
|
|
0
|
0
|
1
|
0
|
undefined
|
1
|
Undefined
|
|
30
|
|
|
|
|
|
2
|
|
45
|
|
|
1
|
1
|
|
|
|
60
|
|
|
|
|
2
|
|
|
90
|
1
|
0
|
undefined
|
0
|
undefined
|
1
|
|
120
|
|
- |
- |
- |
-2
|
|
|
135
|
|
- |
-1
|
-1
|
- |
|
|
150
|
|
- |
- |
- |
- |
2
|
|
180
|
0
|
-1
|
0
|
undefined
|
-1
|
undefined
|
|
210
|
- |
- |
|
|
- |
-2
|
|
225
|
- |
- |
1
|
1
|
- |
- |
|
240
|
- |
- |
|
|
-2
|
- |
|
270
|
-1
|
0
|
undefined
|
0
|
Undefined
|
-1
|
|
300
|
- |
|
- |
- |
2
|
- |
|
315
|
- |
|
-1
|
-1
|
|
- |
|
330
|
- |
|
- |
- |
|
-2
|
|
360
|
Same as 0
|
|
|
|
|
|
We need to discuss how I
filled in values for 0, 90, 180, and 270. These are called quadrantal angles. What
make them different are reference angles and triangles do not exist for these
angles of rotation. Here I rely on the identities we developed earlier:
|
Angle
|
X
|
Y
|
Sin
y
|
Cos
x
|
Tan
Y/x
|
Cot
X/y
|
SEC
1/x
|
CSC
1/y
|
|
0
|
1
|
0
|
0
|
1
|
0
|
undefined
|
1
|
undefined
|
|
90
|
0
|
1
|
1
|
0
|
undefined
|
0
|
undefined
|
1
|
|
180
|
-1
|
0
|
0
|
-1
|
0
|
undefined
|
1
|
undefined
|
|
270
|
0
|
-1
|
-1
|
0
|
undefined
|
0
|
undefined
|
1
|
I think that you will be
better off to develop your skills in creating this table rather than trying to
memorize it. Of course for this on line course, you will have access to it. But
you calc instructor will expect you to be able to arrive at these exact values
fairly readily.