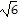 , multiplicity 1, crosses x-axis; -
, multiplicity 1, crosses x-axis; -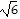 , multiplicity 1, crosses x-axis;
, multiplicity 1, crosses x-axis;2, multiplicity 2, touches x-axis; -2, multiplicity 2, touches x-axis
Exam
Name___________________________________
| MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. | ||
| Form a polynomial whose zeros and degree are given. | ||
| 1) | Zeros: -3, -2, 3; degree 3 | 1) ______ |
| A) f(x) = x3 + 2x2 - 9x - 18 for a = 1 | |
| B) f(x) = x3 + 2x2 + 9x + 18 for a = 1 | |
| C) f(x) = x3 - 2x2 + 9x - 18 for a = 1 | |
| D) f(x) = x3 - 2x2 - 9x + 18 for a = 1 |
| For the polynomial, list each real zero and its multiplicity. Determine whether the graph crosses or touches the x-axis at each x -intercept. | ||
| 2) | f(x) = 5(x + 3)(x + 7)4 | 2) ______ |
| A) 3, multiplicity 1, touches x-axis; 7, multiplicity 4, crosses x-axis | |
| B) -3, multiplicity 1, crosses x-axis; -7, multiplicity 4, touches x-axis | |
| C) -3, multiplicity 1, touches x-axis; -7, multiplicity 4, crosses x-axis | |
| D) 3, multiplicity 1, crosses x-axis; 7, multiplicity 4, touches x-axis |
| 3) | f(x) = 2(x2 + 6)(x2 + 4)2 | 3) ______ |
| A) -6, multiplicity 1, touches x-axis; -4, multiplicity 2, crosses x-axis | |
B)
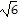 , multiplicity 1, crosses x-axis; - , multiplicity 1, crosses x-axis; -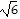 , multiplicity 1, crosses x-axis; , multiplicity 1, crosses x-axis;2, multiplicity 2, touches x-axis; -2, multiplicity 2, touches x-axis |
|
| C) -6, multiplicity 1, crosses x-axis; -4, multiplicity 2, touches x-axis | |
| D) No real zeros |
| Find the x- and y-intercepts of f. | ||
| 4) | f(x) = (x + 6)(x - 4)(x + 4) | 4) ______ |
| A) x-intercepts: -4, 4, 6; y-intercept: 96 | |
| B) x-intercepts: -6, -4, 4; y-intercept: -96 | |
| C) x-intercepts: -6, -4, 4; y-intercept: 96 | |
| D) x-intercepts: -4, 4, 6; y-intercept: -96 |
| Determine the maximum number of turning points of f. | ||
| 5) | f(x) = -x2(x + 6)3(x2 - 1) | 5) ______ |
| A) 2 | |
| B) 7 | |
| C) 5 | |
| D) 6 |
| Use the x-intercepts to find the intervals on which the graph of f is above and below the x-axis. | ||
| 6) | f(x) = (x - 2)2(x + 3)2 | 6) ______ |
|
A)
above the x-axis: no intervals below the x-axis: (-∞, -3), (-3, 2), (2, ∞) |
|
|
B)
above the x-axis: (-∞, -3), (2, ∞) below the x-axis: (-3, 2) |
|
|
C)
above the x-axis: (-3, 2) below the x-axis: (-∞, -3), (2, ∞) |
|
|
D)
above the x-axis: (-∞, -3), (-3, 2), (2, ∞) below the x-axis: no intervals |
| List the potential rational zeros of the polynomial function. Do not find the zeros. | ||
| 7) | f(x) = 11x3 - x2 + 5 | 7) ______ |
A)
± 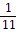 , ± , ± 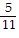 , ± 1, ± 5 , ± 1, ± 5
|
|
B)
± 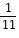 , ± , ± 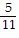 , ± 1, ± 5, ± 11 , ± 1, ± 5, ± 11
|
|
C)
± 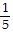 , ± , ± 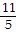 , ± 1, ± 11 , ± 1, ± 11
|
|
D)
± 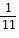 , ± , ± 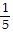 , ± 1, ± 5, ± 11 , ± 1, ± 5, ± 11
|
| Use the Rational Zeros Theorem to find all the real zeros of the polynomial function. Use the zeros to factor f over the real numbers. | ||
| 8) | f(x) = x3 + 2x2 - 5x - 6 | 8) ______ |
| A) -3, -1, 2; f(x) = (x + 3)(x + 1)(x - 2) | |
| B) -1; f(x) = (x + 1)(x2 + x - 6) | |
| C) -3; f(x) = (x + 3)(x2 - x - 2) | |
| D) -2, 1, 3; f(x) = (x + 2)(x - 1)(x - 3) |
| Solve the problem. | ||
| 9) |
A box with an open top is formed by cutting squares out of the corners of a rectangular piece of cardboard and then folding up the sides. If x represents the length of the side of the square cut from each corner, and if the original piece of cardboard is 20 inches by 15 inches, what size square must be cut if the volume of the box is to be 336 cubic inches?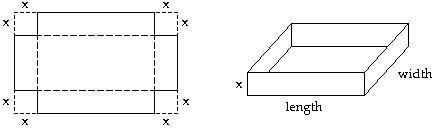
| 9) ______ |
| A) 12 in. by 12 in. | |
| B) 4 in. by 4 in. | |
| C) 7 in. by 7 in. | |
| D) 3 in. by 3 in. |
| Find the domain of the rational function. | ||
| 10) |
g(x) = 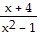
| 10) ______ |
| A) {x|x ≠ -1, x ≠ 1, x ≠ -4} | |
| B) all real numbers | |
| C) {x|x ≠ 0, x ≠ 1} | |
| D) {x|x ≠ -1, x ≠ 1} |
| 11) |
f(x) = 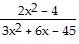 . .
| 11) ______ |
| A) {x|x ≠ 3, x ≠ -3, x ≠ -5} | |
| B) {x|x ≠ 3, x ≠ -5} | |
| C) all real numbers | |
| D) {x|x ≠ -3, x ≠ 5} |
| Use the graph to determine the domain and range of the function. | ||
| 12) |
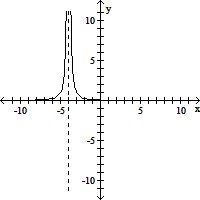 | 12) ______ |
|
A)
domain: {x|x ≥ 0} range: {y|y ≠ -4} |
|
|
B)
domain: {x|x ≠ -4} range: {y|y ≥ 0} |
|
|
C)
domain: {x|x > 0} range: {y|y ≠ -4} |
|
|
D)
domain: {x|x ≠ -4} range: {y|y > 0} |
| Find the vertical asymptotes of the rational function. | ||
| 13) |
g(x) = 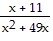
| 13) ______ |
| A) x = 0, x = -49 | |
| B) x = 0, x = -7, x = 7 | |
| C) x = -49, x = -11 | |
| D) x = -7, x = 7 |
| 14) |
f(x) = 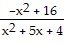
| 14) ______ |
| A) x = 1, x = -4 | |
| B) x = -1, x = 4 | |
| C) x = -1 | |
| D) x = -1, x = -4 |
| Give the equation of the horizontal asymptote, if any, of the function. | ||
| 15) |
g(x) = 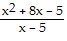
| 15) ______ |
| A) y = 0 | |
| B) y = 1 | |
| C) y = 5 | |
| D) no horizontal asymptotes |
| 16) |
f(x) = 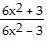
| 16) ______ |
| A) y = 3 | |
| B) y = 1 | |
| C) y = 6 | |
| D) no horizontal asymptotes |
| 17) |
g(x) = 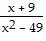
| 17) ______ |
| A) y = 0 | |
| B) y = -7, y = 7 | |
| C) no horizontal asymptotes | |
| D) y = 1 |
| Graph the function. | ||
| 18) |
f(x) = 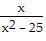 
| 18) ______ |
A)
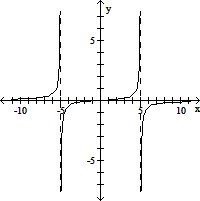
|
|
B)
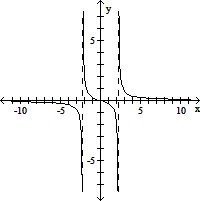
|
|
C)
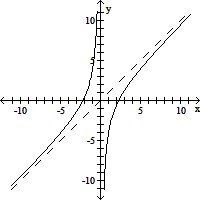
|
|
D)
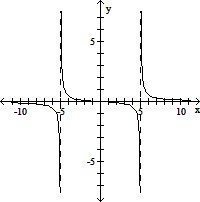
|
| Find the indicated intercept(s) of the graph of the function. | ||
| 19) |
x-intercepts of f(x) = 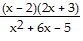
| 19) ______ |
A)
(2, 0), 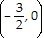
|
|
| B) (2, 0), (-3, 0) | |
C)
(-2, 0), 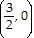
|
|
| D) none |
| Graph the function. | ||
| 20) |
f(x) = 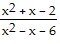 
| 20) ______ |
A)
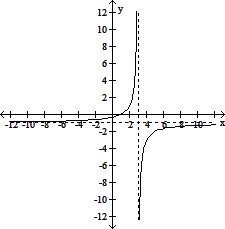
|
|
B)
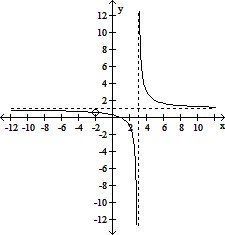
|
|
C)
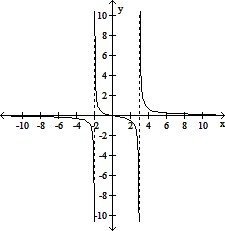
|
|
D)
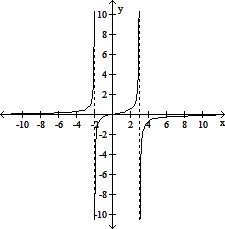
|
| Solve the problem. | ||
| 21) |
Decide which of the rational functions might have the given graph.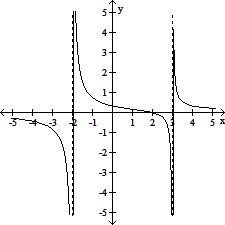
| 21) ______ |
A)
R(x) = 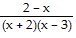
|
|
B)
R(x) = 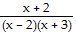
|
|
C)
R(x) = 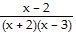
|
|
D)
R(x) = 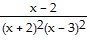
|
| Find the indicated intercept(s) of the graph of the function. | ||
| 22) |
y-intercept of f(x) = 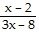
| 22) ______ |
A)
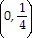
|
|
B)
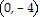
|
|
| C) (0, 2) | |
| D) none |