Exam
Name___________________________________
| MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. | ||
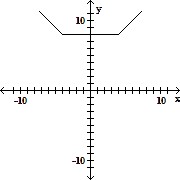
| Determine the intervals on which the function is increasing, decreasing, and constant. | ||
| 1) |

| 1) ______ |
| A) Increasing on (-∞, 4); Decreasing on (-4, ∞); Constant on (4, ∞) | |
| B) Increasing on (4, ∞); Decreasing on (-4, ∞); Constant on (-4, 4) | |
| C) Increasing on (4, ∞); Decreasing on (-∞, -4); Constant on (-4, 4) | |
| D) Increasing on (-∞, 4); Decreasing on (-∞, -4); Constant on (4, ∞) |
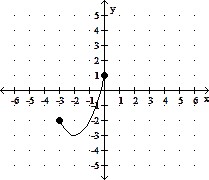
| Determine the domain and range of the function. | ||
| 2) |
| 2) ______ |
| A) domain: (-∞, 1]; range: [0, 3] | |
| B) domain: [-3, 1]; range: [-3, 0] | |
| C) domain: [-3, 0]; range: [-3, 1] | |
| D) domain: [0, 3]; range: (-∞, 1] |
| For the piecewise function, find the specified function value. | ||
| 3) |
f(x) = {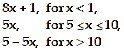 f(5) | 3) ______ |
| A) 25 | |
| B) -20 | |
| C) 9 | |
| D) 51 |
| For the pair of functions, find the indicated domain. | ||
| 4) |
For f(x) = 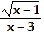 Find the domain of f(x). | 4) ______ |
| A) [0, 3) ∪ (3, ∞) | |
| B) (1, 3) ∪ (3, ∞) | |
| C) [1, 3) ∪ (3, ∞) | |
| D) [1, ∞) |
| Find the average rate of change of the function over the given interval. | ||
| 5) |
y = 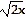 , [2, 8] , [2, 8]
| 5) ______ |
| A) 2 | |
B)
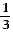
|
|
| C) 7 | |
D)
- 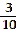
|
| 6) |
Find the intervals where the function is concave up and concave down and the point of inflection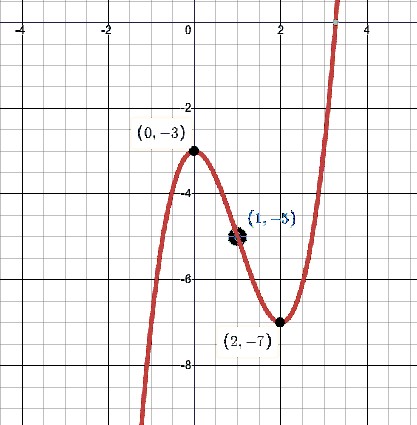
| 6) ______ |
| A) up (1, oo) down (-oo, 1) (1,-5) | |
| B) up (-oo, 1) down (1, oo) (1,-5) | |
| C) up (1,oo) down (-oo, 1) (0, -3) | |
| D) up (1,oo) down (-oo, 1) (2, -7) |
| Solve the problem. | ||
| 7) |
Use the graphs to find the value of (f + g)(3).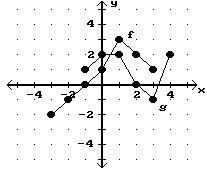
| 7) ______ |
| A) 1 | |
| B) 0 | |
| C) -1 | |
| D) 3 |
| 8) |
Use the tables to find (fg)(-8).  | 8) ______ |
| A) -25 | |
| B) -56 | |
| C) 6 | |
| D) 64 |
| Determine whether or not the function is one-to-one. | ||
| 9) |
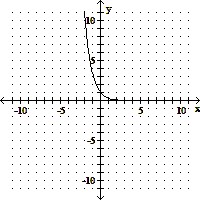
| 9) ______ |
| A) No | |
| B) Yes |
| 10) |
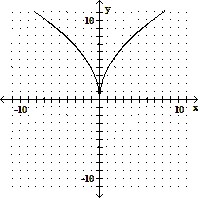
| 10) ______ |
| A) No | |
| B) Yes |
| Decide whether the given functions are inverses. | ||||
| 11) |
| 11) ______ | ||
| A) No | |
| B) Yes |
| 12) |
| 12) ______ |
| A) Yes | |
| B) No |
| Decide whether or not the functions are inverses of each other. | ||
| 13) |
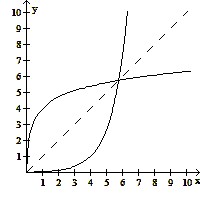
| 13) ______ |
| A) No | |
| B) Yes |
| If f is one-to-one, find an equation for its inverse. | ||
| 14) | f(x) = 7x - 4 | 14) ______ |
A)
f-1(x) = 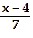
|
|
B)
f-1(x) = 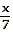 + 4 + 4
|
|
| C) Not a one-to-one function | |
D)
f-1(x) = 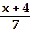
|
| 15) |
f(x) = 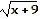 , x ≥ -9 , x ≥ -9
| 15) ______ |
A)
f-1(x) = 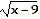
|
|
| B) f-1(x) = x2 - 9, x ≥ 0 | |
| C) Not a one-to-one function | |
| D) f-1(x) = (x + 9)2 |
| 16) |
f(x) = 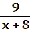
| 16) ______ |
A)
f-1(x) = 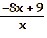
|
|
| B) Not a one-to-one function | |
C)
f-1(x) = 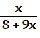
|
|
D)
f-1(x) = 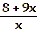
|